This statistical audit was conducted by Jaime Lagüera González, Panagiotis Ravanos, Michaela Saisana, Oscar Smallenbroek and Carlos Tacao Moura, European Commission, JRC, Ispra, Italy.
The process of understanding and modeling the fundamentals of innovation at the national level and across the globe inevitably entails conceptual and practical challenges. Now in its 17th edition, the Global Innovation Index (GII) 2024, considers these conceptual challenges and deals with practical issues – related to data quality and methodological choices – by grouping economy-level data for 133 economies across 78 indicators into 21 sub-pillars, seven pillars, two sub-indices and, finally, an overall index. This appendix offers detailed insights into the practical challenges related to the construction of the GII. In particular, it analyzes the statistical soundness of the conceptual framework and the robustness of calculations and modeling assumptions used to arrive at the final index rankings.
Statistical soundness should be regarded as a necessary but not sufficient condition for a sound GII, since the correlations underpinning the majority of the statistical analyses carried out herein need not “necessarily represent the real influence of the individual indicators on the phenomenon being measured” (
The European Commission’s Competence Centre on Composite Indicators and Scoreboards (COIN) at the Joint Research Centre (JRC) in Ispra, Italy, has been invited to audit the GII for a 14th consecutive year. As in previous editions, the present JRC-COIN audit focuses on the statistical soundness of the multilevel structure of the index, as well as on the impact of key modeling assumptions on the results.
As in the previous GII reports, the JRC-COIN analysis complements the economy rankings of the GII, the Innovation Input Sub-Index and the Innovation Output Sub-index with confidence intervals, in order to allow a better appreciation of the robustness of these rankings to the choice of computation methodology. The JRC-COIN analysis also includes an assessment of the added value of the GII and it supplements the GII scores with a measure of the “distance to the performance frontier” of innovation through the use of data envelopment analysis.
Step 1 Conceptual consistency
compatibility with existing literature on innovation and pillar definition
use of scaling factors per indicator to present a fair picture of economy differences (e.g., GDP, population)
Step 2 Data checks
check for data timeliness (90 percent of available data refer to 2021 or a later year)
inclusion requirements per economy (availability of 66 percent for the Input and the Output Sub-Indices separately and data availability for at least two sub-pillars per pillar)
check for reporting errors (interquartile range)
outlier identification (skewness and kurtosis) and treatment (winsorization or logarithmic transformation)
direct contact with data providers
Step 3 Statistical coherence
treatment of pairs of highly collinear variables as a single indicator
assessment of grouping of indicators into sub-pillars, pillars, sub-indices and the GII
use of weights as scaling coefficients to ensure statistical coherence
assessment of arithmetic average assumption
assessment of potential redundancy of information in the overall GII
Step 4 Qualitative review
internal qualitative review (by WIPO in partnership with the Portulans Institute, the GII Corporate and Academic Network partners, as well as the GII Advisory Board members)
a one-off qualitative audit (by the WIPO Internal Oversight Section)
(2)Available at: www.wipo.int/export/sites/www/about-wipo/en/oversight/docs/iaod/audit/audit-gii-exec-summary.pdf, IOD Ref: IA 2022-03, April 14, 2023. external qualitative review (by JRC-COIN and international experts)
Source: European Commission, Joint Research Centre, 2024.
Conceptual and statistical coherence within the GII framework
The GII model was assessed by the JRC-COIN in June 2024. Suggestions for fine-tuning certain aspects were taken into account in the final computation of the rankings during an iterative process with the JRC-COIN aiming to set the foundations for a balanced index. This four-step process is outlined in Box 1.
Step 1: Conceptual consistency
A total of 78 indicators were selected for their relevance to specific innovation pillars, based on a literature review, expert opinion, economy coverage and timeliness. To present a fair picture of economy differences, indicators were scaled either at source or by the GII team, as appropriate and where needed. For example, Expenditure on education (indicator 2.1.1) is expressed as a percentage of GDP, while Government funding per pupil at secondary level (indicator 2.1.2) is expressed as a percentage of GDP per capita. On the advice of JRC-COIN, the GII developers normalized nine more indicators to a 0–100 range in the 2023 edition, so that all indicators have the same range, which facilitates their individual contributions to the overall index score.
The 2024 edition of the GII includes some changes to the indicators.
The number of indicators considered is 78 instead of 80. The Cost of redundancy dismissal, indicator 1.2.3. in last year’s edition, was dropped from the Regulatory environment sub-pillar (1.2). This change was informed by a thorough literature review revealing weak fitness of the indicator with the concept of innovation, as well as concerns about its timeliness. The sub-pillar now includes two equal-weighted indicators (1.2.1 Regulatory quality and 1.2.2 Rule of law). Additionally, Generic top-level domains (TLDs) and Country-code TLDs (indicators 7.3.1 and 7.3.2 of the Online creativity sub-pillar 7.3 in the 2023 edition) have been merged into a single indicator representing the sum of generic top-level domains (TLDs) and country-code TLDs.
In sub-pillar 3.3 Ecological sustainability a new indicator, Low-carbon energy use (3.3.2), has replaced the Environmental performance indicator based on a more stringent fit with the concept of innovation.
In sub-pillar 5.2 Innovation linkages, indicator Public Research–Industry co-publications (5.2.1), has replaced the Gross domestic Expenditure on R&D (GERD) financed by abroad indicator, based on concerns about the timeliness and future data availability of the latter.
The computation methodology of indicators 3.1.1 ICT access and 3.1.2 ICT use has changed. These two variables are themselves composite indices computed by WIPO and their composition has been changed slightly to better reflect the current discussions at the International Telecommunications Union (ITU), which provides the raw data for these indicators.
The source of data for the indicator 4.3.1 Applied tariff rate has changed from the World Bank to the World Trade Organization.
Finally, indicator 1.3.1 Policies for doing business has been renamed Policy stability for doing business.
The above changes highlight the developer’s meticulous attention to the monitoring, evaluating and updating of the theoretical framework and the data sources used for the index, with an aim to provide an even more robust and timely measure of innovation performance.
Step 2: Data checks
The data used for each economy were those most recently released within the period 2013 to 2024, with 90 percent of the available data refer to 2021 or a later year. With regards to the inclusion of countries in the GII, the 2024 edition follows the criteria adopted in 2016,
In practice, data availability for all economies included in the GII 2024 is quite satisfactory: At least 80 percent of data is available for 81 percent of the economies covered (equivalent to 108 economies out of 133), while 75% of the considered indicators are available for 95% of the economies covered.
Potentially problematic indicators that could bias the overall results were identified on the basis of two measures related to the shape of the data distributions: skewness and kurtosis. In 2011, a joint decision by the GII team and the JRC-COIN determined that values would be treated if an indicator had absolute skewness greater than 2.0 and kurtosis greater than 3.5.
for indicators with absolute skewness greater than 2.25 and kurtosis greater than 3.5, apply either winsorization or the natural logarithm (in cases of more than five outliers);
for indicators with absolute skewness less than 2.25 and kurtosis greater than 10.0, produce scatterplots to identify potentially problematic values that need to be considered as outliers and treated accordingly.
For a total of 27 indicators, one up to 5 values were winsorised, while for an additional 5 indicators (2.3.3 Global corporate R&D investors, 4.2.2 Venture capital investors, 5.2.5. Patent families, 6.1.1 Patents by origin and 7.3.3 Mobile app creation) the natural logarithm was applied. For two of these five indicators (4.2.2 Venture capital investors and 5.2.5. Patent families) the values of skewness and kurtosis did not abide by the set thresholds after applying the natural logarithm transformation.
Step 3: Statistical coherence
Weights as scaling coefficients
The JRC-COIN and GII team jointly decided in 2012 that weights of 0.5 or 1.0 were to be used as scaling coefficients and not importance coefficients, with the aim of arriving at sub-pillar and pillar scores that were balanced in their underlying components (i.e., that indicators and sub- pillars can explain a similar amount of variance in their respective sub-pillars/pillars).
As a result of this analysis, two sub-pillars are also given a weight of 0.5 – 7.2 Creative goods and services and 7.3 Online creativity. In the previous edition of the GII, a weight of 0.5 was also applied to two indicators of the input sub-pillar 1.2 Regulatory environment – 1.2.1 Regulatory quality and 1.2.2 Rule of law – but this was amended in this edition of the index. This change is due to the removal of indicator 1.2.3 from the same sub-pillar (which in the previous edition of the index had a weight of 1).
Despite this weighting adjustment, two indicators (5.3.4 FDI net inflows and 6.2.1 Labor productivity growth) were found to be non-influential in this year’s GII framework, meaning that they could not explain at least 9 percent of economies’ overall variation in the respective sub-pillar scores.
Principal component analysis and reliability item analysis
Principal component analysis (PCA) was used to assess the extent to which the conceptual framework is confirmed by statistical approaches. PCA results confirm the presence of a single latent dimension in each of the seven pillars (one component with an eigenvalue greater than 1.0) that captures between approximately 59 percent (pillar 3: Infrastructure) and up to 83 percent (pillar 5: Business sophistication) of the total variance in the three underlying sub-pillars. Furthermore, results confirm the expectation that in the majority of the cases, the sub-pillars are more closely correlated with their own pillar than with any other pillar and that all correlation coefficients are close to or greater than 0.70 (Appendix Table 2).
The five input pillars share a single statistical dimension that summarizes 81 percent of the total variance and the five loadings (correlation coefficients) of these pillars are very similar to each other. This similarity suggests that the five pillars make a roughly equal contribution to the variation of the Innovation Input Sub-Index scores, as envisaged by the development team. Consequently, the reliability of the Input Sub-Index, measured by Cronbach’s alpha value, is very high at 0.93 – well above the 0.70 threshold for a reliable aggregate (
The two output pillars – Knowledge and technology outputs and Creative outputs – are strongly correlated with each other (0.86); they are also both strongly correlated with the Innovation Output Sub-Index (0.96 and 0.97).
Finally, the two sub-indices are equally important in the overall GII. The GII is built as a simple arithmetic average of the Input Sub-Index and the Output Sub-Index. In fact, the Pearson correlation coefficients of the two sub-indices with the GII (0.97 in both cases), and the correlation between themselves (0.90), suggests that they are effectively placed on an equal footing.
Concluding remarks
Overall, the statistical analysis in this section demonstrates that the grouping of variables into sub-pillars, pillars and an overall index is statistically coherent within the GII 2024 framework and that the GII has a balanced structure at each aggregation level. Furthermore, in this edition of the index, the JRC-COIN found robust evidence of insufficient influence on the GII framework only for two of the 78 indicators (5.3.4 FDI net inflows and 6.2.1 Labor productivity growth) – that is, each of these two indicators explains less than 9 percent of countries’ variation in their respective sub-pillar scores.
Added value of the GII
High statistical association between the components of a composite index could be interpreted by some as a sign of redundancy of information within the composite index. For the case of the GII, the Input and Output Sub-Indices correlate strongly with each other and with the overall GII, while the five pillars in the Input Sub-Index have a very high statistical reliability. However, the tests conducted by the JRC-COIN confirm that this high statistical reliability does not result in redundancy of information. In particular, a country’s GII ranking differs from that in any of the seven pillars by 10 positions or more at least 39 percent (up to 70 percent) of the 133 economies included in the GII 2024 (Appendix Table 3). This serves as a demonstration of the added value of the GII ranking, which helps to highlight other aspects of innovation within individual countries that are not immediately apparent from analysis of the seven pillars individually. It also highlights the usefulness of taking due account of the information contained in each of the GII pillars, sub-pillars and indicators individually. By doing so, economy-specific strengths and bottlenecks in terms of innovation can be identified and serve as a basis for evidence-based policymaking.
Step 4: Qualitative review
Lastly, JRC-COIN evaluated the GII results – in particular, the overall economy classifications and relative performances in terms of the Innovation Input or Output Sub-Indices – with the aim to verify that the overall results are robust with respect to the modeling assumptions made during the construction of the GII. Robustness is a powerful characteristic for a composite index as it verifies its reliability as a monitoring framework of the underlying phenomenon that is being measured. Overall, the results in this section verify the robustness of GII with respect to modeling assumptions and its reliability as a monitoring framework for innovation performance. Notwithstanding these positive results, the structure of the GII model is, and has to remain, open to future improvements which may be needed as better data, more comprehensive surveys and assessments, and new, relevant research studies become available.
The impact of modeling assumptions on the GII results
An important part of the GII statistical audit is to check the effect of varying assumptions within plausible ranges. Modeling assumptions with a direct impact on GII scores and rankings relate to:
the underlying structure selected for the index based on pillars;
the choice of individual variables to be used as indicators;
decisions regarding whether (and how) to impute missing data;
decisions regarding whether (and how) to treat outliers;
the selection of the normalization formula to be used;
the choice of aggregation weights for indicators and their aggregates; and
the aggregation rule to be used at each different level of the index structure.
The rationale for the choices made by the GII developers regarding each of these issues is well-grounded: for instance, expert opinion coupled with statistical analysis informs the selection of the individual indicators; common practice and easier interpretation suggest the use of a minimum–maximum normalization approach in the [0–100] range; statistical analysis guides the treatment of outliers; while simplicity and parsimony criteria advocate for the developers’ choice for not imputing missing data. The uncertainty that naturally stems from the above-mentioned modeling choices is accounted for in the robustness assessment carried out by the JRC-COIN. In particular, the methodology applied allows for the joint and simultaneous analysis of the impact of such choices on the aggregate scores. The analysis carried out by JRC-COIN supplements the GII 2024 individual economy rankings with confidence intervals, to better appreciate the robustness of these ranks to the modeling choices.
As suggested by the relevant literature on composite indicators,
The Monte Carlo simulation comprised 5,000 runs of different sets of weights for the seven GII pillars. Weights were assigned to the pillars based on random perturbations centered on the reference values. The ranges of simulated weights were defined by considering both the need for a wide enough interval to allow for meaningful robustness checks and the need to respect the underlying principle of the GII that the Input and the Output Sub-Indices should be placed on an equal footing. As a result of these considerations, the limit values of uncertainty for the five input pillars are between 10 and 30 percent, whereas the limit values for the two output pillars are between 40 and 60 percent (Appendix Table 4).
For transparency and replicability purposes, the GII team has always opted not to estimate missing data. In the cases where missing data exist, the score of the aggregate containing the missing value is based on the other elements of the aggregate for which values are observed. This “no imputation” choice is common in similar contexts and is usually selected to improve transparency and avoid any methodological black box in the imputation of data. Technically, this constitutes a form of “shadow” imputation (for example, in an arithmetic average it is equivalent to replacing the missing value with the arithmetic average of the elements for which values are observed). Hence, the available data (indicators) in the incomplete pillar may dominate, sometimes biasing the ranks up or down. To test the impact of not imputing missing values, the JRC-COIN estimated missing data using two different data imputation approaches: (a) the expectation–maximization (EM) algorithm and (b) the nearest neighbor (k-NN) approach (using the five nearest neighbors). Both these were applied within each GII pillar and then compared to the no-imputation approach (see Appendix Table 6).
Regarding the aggregation formula, decision-theory practitioners challenge the use of simple arithmetic averages because of their fully compensatory nature, where a country’s high comparative advantage on a few indicators can compensate for its comparative disadvantage on many other indicators (
Six models were tested based on the combination of no imputation versus EM or k-NN imputation and arithmetic versus geometric average. A random combination of these choices plus a random set of perturbed weights were used in a total of 5,000 simulations for the GII and each of the two sub-indices (see Appendix Table 4 for a summary of the uncertainties considered).
Uncertainty analysis results
The main results of the robustness analysis are shown in Appendix Figure 1, with median ranks and 90 percent confidence intervals computed across the 5,000 Monte Carlo simulations for the GII and the two sub-indices. Economies are in ascending order (best to worst performing) according to their reference rank (black line), with the dot representing the median rank over the simulations.
Appendix Figure 1 Robustness analysis of the GII, Input and Output Sub-Indices
All published GII 2024 ranks lie within the simulated 90 percent confidence intervals and for most economies these intervals are sufficiently narrow to allow meaningful inferences to be drawn: For 72 of the 133 economies the width of the 90% GII rank confidence interval is less than 10 positions in rank, while this holds for 94 of the 133 economies in the case of the Input Sub-Index and for 96 economies in the case of the Output Sub-Index. However, it is also true that a few economies experience significant changes in rank with variations in weights and aggregation formula and when imputing missing data. Five economies – Qatar, Madagascar, the Islamic Republic of Iran, Barbados and Brunei Darussalam – have 90 percent confidence interval widths of more than 20 positions (21, 23, 24, 29 and 35 positions, respectively). Consequently, their rankings (49th, 110th, 64th, 77th and 88th) in the GII classification should be interpreted cautiously and not taken at face value. However, this is a remarkable improvement compared to GII versions up to 2016, when more than 40 economies had confidence interval widths of more than 20 positions. The improvement in the confidence that can be placed in the GII 2024 ranking is the direct result of the decision to adopt a more stringent criterion for an economy’s inclusion since 2016, which now requires at least 66 percent data availability within each of the two sub-indices.
In a similar fashion, some caution is also warranted with regards to the ranking of four economies (Belarus, Iran, Bolivia and Cabo Verde) for the Input sub-index, for which the 90 percent confidence interval has a width of more than 20 positions (22, 27, 31, and 34). A similar degree of caution is needed in the Output sub-index for three economies – Guatemala, Barbados, and Ghana – which have 90 percent confidence interval widths of more than 20 positions (up to 31 for Ghana). The higher data availability in the Output sub-index in the latest GII editions has contributed to reducing the number of countries with very wide intervals compared to previous editions (e.g., the GII 2019 edition in which there were 13 countries with confidence intervals wider than 20 positions).
Although the rankings for a few economies in the GII or in the two sub-indices appear to be sensitive to methodological choices, the published rankings for the vast majority of the 133 countries included in the 2024 GII can be considered as representative of the plurality of scenarios simulated in this audit. Taking the median rank as the benchmark for an economy’s expected rank in the realm of the GII’s unavoidable methodological uncertainties, 81 percent of the economies are found to shift fewer than three positions with respect to the median rank in the GII; the percentage for the Input and the Output Sub-Indices is similarly large (at 78 and 76 percent respectively).
In order to offer full transparency and complete information, Appendix Table 5 reports the GII 2024 Index and Input and Output Sub-Indices’ economy ranks together with the simulated 90 percent confidence intervals to allow a better appreciation of the robustness of the results to the choice of weights and aggregation formula and the impact of estimating missing data (where applicable).
Sensitivity analysis results
Complementary to the uncertainty analysis, sensitivity analysis has been used to identify which of the modeling assumptions have the greatest impact on certain country rankings. Appendix Table 6 summarizes the impact of changes in the imputation method (EM or k-NN imputation) and/or the aggregation formula (geometric aggregation), keeping the aggregation weights fixed at their reference values (as in the nominal GII). Similar to the results of previous audits, neither the GII nor the Input or Output Sub-Indices are found to be heavily influenced by the imputation of missing data, or by the aggregation formula. In the case of the Input Sub-Index, there exists a group of three economies, Bolivia, Cabo Verde and the Islamic Republic of Iran – that shift rank by more than 20 positions when a different imputation method is used (EM or k-NN instead of no imputation). For Bolivia and Cabo Verde, this can be, at least in part, attributed to their large share of missing data for the Input Sub-Index, as data are available for less than 72 percent of the Input Sub-Index indicators for these economies. The Islamic Republic of Iran on the other hand has a better data availability (86 percent). The choice of the imputation method appears to also be crucial for the ranking of two other countries in the case of the Output Sub-Index, namely Ghana and Côte d'Ivoire. For these countries, missing data account for 16 and 12 percent of the Output Sub-Index indicators.
Overall, the analysis carried out by JRC-COIN verifies that the rankings of the 2024 GII are reliable and, for most economies, the simulated 90 percent confidence intervals are narrow enough to allow meaningful inferences to be drawn for their relative performance. There are a few countries that appear to be sensitive to the way missing values are treated, most of which have a rather large share of missing data. It is however suggested that the readers of the GII 2024 report consider an economy’s ranking in the GII 2024 and in the Input and Output Sub-Indices not only at face value, but also within the 90 percent confidence intervals, in order to better appreciate the degree to which an economy’s rank depends on modeling choices.
These confidence intervals also have to be taken into account when comparing economy rank changes from one year to the next at the GII or Innovation Sub-Index level in order to avoid drawing erroneous conclusions about an economy’s rise or fall in the overall classifications. Since 2016, following the JRC-COIN recommendation in past GII audits, the developers’ decision to apply the 66 percent indicator coverage threshold separately to the Input and Output Sub-Indices in the GII has led to a net increase in the reliability of economy rankings for both the GII and the two sub-indices. Furthermore, the adoption in 2017 of less stringent criteria for skewness and kurtosis (greater than 2.25 in absolute value and greater than 3.5, respectively) has not introduced any bias into the estimates.
Best-practice frontier in the GII by data envelopment analysis
Is there a way to benchmark economies’ multidimensional performance on innovation without imposing a fixed and common set of weights that may be unfair to a particular economy?
Several policy-related aspects of innovation activity at the national level entail an intricate balance between global priorities or drivers and economy-specific strategies and challenges. Comparing multidimensional performance on innovation by subjecting all economies to a common set of weights may prevent acceptance of an innovation index on the grounds that the selected weighting scheme may be unfair to a particular economy, in the sense that it does not reflect its national priorities or the particular challenges that it may be facing vis-à-vis other economies. An appealing feature of the data envelopment analysis (DEA) literature applied in real decision-making settings is the determination of endogenous weights that maximize the overall score of each decision-making unit given a set of other observations. In the absence of a global consensus or strategy regarding the priorities of innovation activity, and with a plethora of national innovation strategies taking place under the effect of various country-specific factors, this approach appears as a reasonable alternative to that of common weights across economies.
In this section, the assumption of fixed pillar weights common to all economies is relaxed once more and, this time, economy-specific weights that maximize an economy’s global innovation score are determined endogenously by means of the Benefit-of-the-Doubt (BoD) model, a tailored DEA model that is suitable for the case of composite indicators construction.
A question that arises from the GII approach is whether there is a way to benchmark economies’ multidimensional performance on innovation without imposing a fixed and common set of weights that might not be fair to a particular economy. The original question in the DEA literature was how to measure each unit’s relative efficiency in production compared to a sample of peers, given observations on input and output quantities and, often, no reliable information on prices (Charnes and Cooper, 1985). A notable difference between the original DEA question and the one applied in the BoD model and used here is that no differentiation between inputs and outputs is made (Cherchye et al., 2008; Melyn and Moesen, 1991). Thus, along the lines of Cook et al. (2014), the BoD model evaluates countries with respect to a best-practice frontier formed by the countries with the relatively best achievements in the considered Pillars, rather than an efficiency frontier formed by the countries that transform inputs to outputs in the most efficient way. To estimate DEA-BoD-based distance to the best-practice frontier scores, we consider the m = 7 pillars in the GII 2024 for n = 133 economies, with yij the value of pillar j in economy i. The objective is to combine the pillar scores per economy into a single number, calculated as the weighted average of the m pillars, where wj represents the weight of the j-th pillar. In the absence of reliable information about the true weights, the weights that maximize the DEA-BoD-based scores are endogenously determined. This gives the following linear programming problem for each economy i:
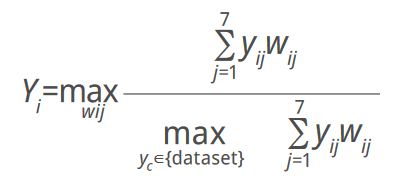
(bounding constraint), subject towij ≥ 0, where, j = 1,…,7, i = 1,…,133 (non-negativity constraint).In this basic programming problem, the weights are non-negative and an economy’s score is between 0 (worst) and 1 (best). The programming problem used to calculate the DEA-BoD socres in this audit included also the restrictions:0.2 ≥ (wij*yij)/Σ(wij*yij) ≥ 0.05, j = 1,…,7 (contribution restrictions).
In theory, each economy is free to decide on the relative weight of each innovation pillar to its score, so as to achieve the best possible score in a computation that reflects its innovation strategy. In practice, the DEA-BoD method assigns a higher (lower) weightto those pillars in which an economy is relatively strong (weak). Reasonable constraints are applied to the weights to preclude the possibility of an economy achieving a perfect score by assigning a zero weight to weak pillars: for each economy, the share of each pillar score (i.e., the pillar score multiplied by the DEA-BoD weight over the total score) has lower and upper bounds of 5 percent and 20 percent, respectively. The DEA-BoD score is then measured as the weighted average of all seven innovation pillar scores, where the weights are the economy-specific DEA-BoD weights, compared to the best performance among all other economies with those same weights. The DEA-BoD score can be interpreted as a measure of the “distance to the best-practice frontier.”
Appendix Table 7 presents pie shares and DEA scores for the top 25 economies in the GII 2024 alongside their respective GII 2024 rankings. All pie shares are in accordance with the starting point of granting leeway to each economy when assigning shares, while not violating the (relative) upper and lower bounds. In this year, Switzerland, Sweden and Singapore are the only economies to obtain a perfect DEA-BoD score of 1.00, indicating that they define the best-practice frontier (in the 2023 GII, the United States was a frontier economy as well). The United States (0.98), the Republic of Korea (0.95) and Finland (0.95) follow in terms of relative performance, very close to the best-practice frontier.
The contribution of the seven pillars to the performance score is quite diverse across the top-25 economies, reflecting the likely different priorities within national innovation strategies. These pie shares can also be seen to reflect different economies’ comparative advantage in certain GII pillars vis-à-vis all other economies and all pillars. For example, China, France and Japan, obtain the same performance score (0.87) but China allocates 20 percent of its DEA score to the Knowledge and technology outputs pillar and 7 percent in the Creative outputs pillar, while quite the opposite holds for France (5 and 20 percent respectively). On the other hand, Japan allocates 5 percent of its DEA-BoD score to both Output pillars, while it allocates between 12 and 20 percent to the five Input pillars. In addition, the Business Sophistication pillar contributes 20 percent of China and Japan’s performance score while only 10 percent of France’s, while Human capital and Research accounts for 18 to 20 percent in the case of France and Japan but 8 percent in the case of China. Appendix Figure 2 shows how close the DEA scores and the GII 2024 scores are for all 133 economies (Pearson correlation of 0.995).
Conclusion
The JRC-COIN analysis suggests that the conceptualized multilevel structure of the GII 2024 – with its 78 indicators, 21 sub-pillars, seven pillars and two sub-indices comprising the overall index – is statistically sound and balanced: that is, each sub-pillar makes a similar contribution to the variation of its respective pillar. The refinements made by the developing team over the years have helped to enhance the already strong statistical coherence within the GII framework, in which the capacity of the 78 indicators to distinguish between economies’ performances is maintained at the sub-pillar level or lower in all but two cases.
The decision not to impute missing values, which is common in comparable contexts and justified on the grounds of transparency and replicability, can at times have an undesirable impact on some economies’ scores, with the additional negative side-effect that it might encourage economies not to report low data values. The GII team’s adoption, in 2016, of a more stringent data coverage threshold (at least 66 percent data availability for each of the input- and output-related indicators) has notably improved confidence in the economy ranking for the GII and the two sub-indices. Moreover, the results of the analysis carried out by JRC-COIN suggest that the developer’s decision not to impute missing values has a notable impact in the rankings of only a very small set of countries and only for the case of the Input or the Output Sub-Indices.
Additionally, the GII team’s decision, in 2012, to use weights as scaling coefficients during index development constitutes a significant departure from the traditional, yet erroneous, vision of weights as a reflection of indicators’ importance in a weighted average. It is hoped that such an approach will be adopted by other developers of composite indicators to avoid situations where bias sneaks in when least expected.
The JRC-COIN analysis also verified that the strong correlations observed between the GII components do not result in a redundancy of information within the GII. For more than 39 percent (up to 70 percent) of the 133 economies included in the GII 2024, the GII ranking and the rankings of any of the seven pillars differ by 10 positions or more. This demonstrates the added value of the GII ranking, which helps to highlight other components of innovation not immediately apparent from a separate analysis of each pillar. At the same time, this finding points to the value of paying particular attention to the GII pillars, sub-pillars and their constituent indicators individually. By doing so, economy-specific strengths and bottlenecks in innovation can be identified and serve as an input for evidence-based policymaking.
All published GII 2024 rankings lie within the simulated 90 percent confidence intervals that take into consideration the unavoidable uncertainties inherent in an estimation of missing data, the weights (fixed vs. simulated) and the aggregation formula (arithmetic vs. geometric average) at the pillar level. For the majority of economies, such intervals are narrow enough for meaningful inferences to be drawn: the intervals comprise 10 or fewer positions for 72 out of the 133 considered economies. The GII rankings of five countries – Qatar, Madagascar, the Islamic Republic of Iran, Barbados and Brunei Darussalam – should however be interpreted with some caution, as they appear to be highly sensitive to the methodological choices. The Input and Output Sub-Indices have the same modest degree of sensitivity to the methodological choices relating to the imputation method, weights or aggregation formula. Economy ranks, either in the GII 2024 or in the two sub-indices, can be considered to be representative of the many possible scenarios: 81 percent of the economies shift fewer than three positions with respect to the median rank within the GII, 78 percent within the Input Sub-Index and 76 percent within the Output Sub-Index.
All things considered, the present JRC-COIN audit findings confirm that the GII 2024 meets international quality standards for statistical soundness, which indicates that it is a reliable benchmarking tool for innovation practices at the economy level around the world.
Finally, the “distance to the best-practice frontier” measure, calculated using data envelopment analysis, can be used as a suitable alternative approach to benchmarking economies’ multidimensional performance on innovation, without imposing a fixed and common set of weights that may be unfair to a particular economy. The results of this analysis are very closely correlated with the nominal GII ranking, while at the same time allowing economies to select their best-possible pillar weights that better highlight their relative strengths and potential national priorities.
The GII should not be considered as the ultimate and definitive ranking of economies with respect to innovation. On the contrary, the GII best represents an ongoing attempt to find metrics and approaches that capture the richness of innovation more effectively, continuously adapting the GII framework to reflect the improved availability of statistics and the theoretical advances in the field. In any case, the GII should be regarded as a sound attempt, based on the principle of transparency, matured over 17 years of constant refinement, to pave the way for better and more informed innovation policies worldwide.
